More on Fibonacci Numbers
Most Forex traders are familiar with Fibonacci numbers and their use in Forex pricing. But Fibonacci is actually one of the most famous names in mathematics and his number sequences have been around for quite a while.
So who is Fibonacci? While the name, Leonard Fibonacci, has been credited as the developer of this mathematical accomplishment, his real name was Leonardo Pisano. Leonardo Pisano was born late in the twelfth century in Pisa, Italy (Pisano in Italian indicated that he was from Pisa). His father was a merchant by the name of Guglielmo Bonaccio and it’s because of this name that Leonardo Pisano became known as Fibonacci. When scholars centuries later were studying the hand written copies of Liber Abaci, published before printing was invented, they misinterpreted part of the title – “filius Bonacci” meaning “son of Bonaccio” – as his surname, and the name Fibonacci was born.
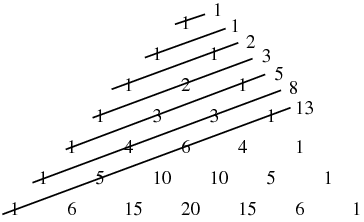
The famous sequence – 0, 1, 1, 2, 3, 5, 8, 13, for which he has been immortalized was actually not what he set out to realize. Rather, he considered something else his greatest mathematical achievement, i.e. helping to popularize our modern number system in the Latin-speaking world.
The Roman numeral system used by the Roman Empire was not displaced until the mid-13th Century AD, and Leonardo Pisano’s book, Liber Abaci (which means “The Book of Calculations”), was one of the first Western books to describe their eventual replacement.
Rabbits
The impact of Fibonacci’s book at the beginning of the spread of decimal numbers was a great mathematical feat. But Fibonacci is better remembered for a certain sequence of numbers that appeared as an example in Liber Abaci. And this began with an experiment involving rabbits and how fast they could breed. He took a newly-born pair of rabbits, one male, one female, and at the end of one month they mated. Assuming the rabbits never died and that the female always produced one new pair (one male, one female) every month from the second month on, how many pairs would there be in one year?
And here’s how he got to his famous sequence:
At the end of the first month, they mate, but there was still only 1 pair.
At the end of the second month the female produced a new pair, so now there were 2 pairs of rabbits.
At the end of the third month, the original female produced a second pair, making 3 pairs in all.
By the end of the fourth month, the original female had produced yet another new pair and the female born two months before produced her first pair also, making a total of 5 pairs.
Now imagine that there are pairs of rabbits after months. The number of pairs in month n+1 will be (in this problem, rabbits never die) plus the number of new pairs born. But new pairs are only born to pairs at least 1 month old, so there will be new pairs. So we have which is simply the rule for generating the Fibonacci numbers: add the last two to get the next. Following this through you’ll find that after 12 months (or 1 year), there will be 233 pairs of rabbits.
Hence the famous mathematical sequence–0, 1, 1, 2, 3, 5, 8, 13,….and the Golden Rule which involves taking the ratio of two successive numbers in Fibonacci’s series, dividing each by the number before it, and getting the following series of numbers: 1/1 = 1, 2/1 = 2, 3/2 = 1.5, 5/3 = 1.666…, 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.61538… Fibonacci’s Golden Rule continues to be used in many spheres such as finance, biology, ecology and more.